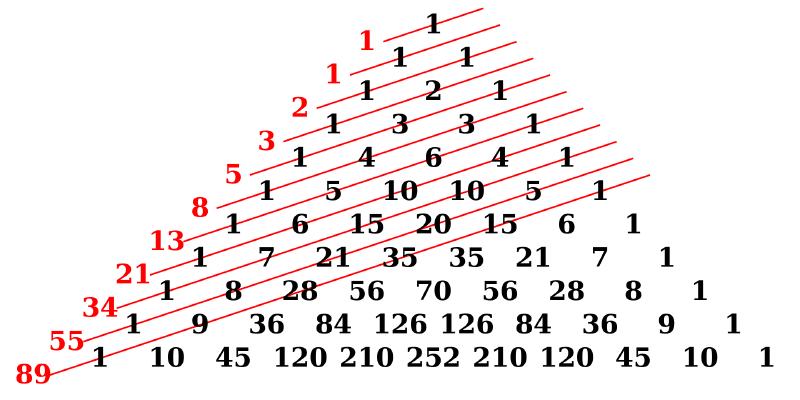
动态规划实现有两种方法：

1. 自下而上        (制表)
2. 自上而下        (记忆化)

自下而上

自下而上是通过 迭代 实现的

以斐波那契数列为例，F(0)=0, F(1)=1。通过F(0)和F(1)计算F(2)，然后使用计算结果计算F(3)…

以此类推，一直计算F(n)

1
2
3
4
5
6
7

// 伪代码如下:

F = array of length (n + 1)
F[0] = 0
F[1] = 1
for i from 2 to n:
    F[i] = F[i - 1] + F[i - 2]

自上而下

自上而下通过 递归 实现，并且通过 记忆化 提高效率(之后解释记忆化概念)

如果我们想知道斐波那契数列F(n)，需要找到F(n-1)和F(n-2)…通过递归求出F(0)和F(1)

缺点也很明显，在计算中存在大量的 重复计算 ，导致效率不高

而解决方法也很简单，用空间换时间，也就是 记忆化 ：将函数调用的结果存储在哈希图或数组中，这样当再次进行相同的函数调用时，我们可以简单地返回记忆的结果，而不是重新计算结果。

1
2
3
4
5
6
7
8
9

//伪代码如下:
 
memo = hashmap
Function F(integer i):
    if i is 0 or 1: 
        return i
    if i doesn't exist in memo:
        memo[i] = F(i - 1) + F(i - 2)
    return memo[i]

总结

所以，这两个算法哪个更好呢？

DP(动态规划问题)可以用任意一种方法实现

每个方法都有一个突出的优点:

• 自下而上的运行速度更快    (递归效率低)
• 自上而下的实现更简单        (因为对于递归来说，我们不用在意子问题的逻辑顺序，而对于自下而上的方法来说，我们需要解决子问题的逻辑顺序)

比较简单而且经典的题目：《力扣 62.不同路径》

学习资料如下:

Explore - LeetCode

如有遗漏或错误，欢迎补充纠正